La inversa de una función se obtiene cambiando el orden de x por y en las parejas y viceversa, es decir, (x,y) por (y,x). Tomando en cuenta que:
- Para definir la inversa de una función, ésta debe ser inyectiva.
- La inversa de una función, se necesita que sea biyectiva (inyectiva y sobreyectiva) para que se considere como una función.
Si f es una función inyectiva considerada como el conjunto (x,y), esta función tiene una función inversa denotada como f -1 siendo el conjunto de (y,x) el que lo conforma. Se cumple que el dominio de f-1 es el contradominio de f y que el contradominio de f-1 es el dominio de f.
Ejemplos:
°
°
°
° 
° 
° 
° 
° 
° 
Probar que: 
Probar que: 
°
Probar que: 
Determinación de la inversa de una función.-
Paso 1) Encuentrar el dominio de f y verificar que la función sea inyectiva. Si no es inyectiva, no hay que continuar, ya que no existe f-1 , o determinar un intervalo en el cual la función sea uno a uno, y ahí sí se podrá encontrar la inversa.
Paso 2) Intercambiar x por y en f y despejar a y, esta será f-1 .
Paso 3) Encontrar el dominio de f-1 ,éste debe ser igual que el rango de f. Para verificar que la inversa es la correcta basta con realizar la composición de las funciones y que en ambas el resultado sea la función identidad, representado como:
f o f-1 (x) = f(f-1(x)) = x
f-1 o f(x) = f-1 (f(x)) = x
Definición formal de la función inversa.-
Si f es una función uno a uno, entonces la inversa de f, se denota por f-1 , que es la función formada al invertir todos los pares ordenados en f, por consiguiente f-1 = {(y,x) | (x,y) está en f}. Si f no es una función uno a uno, entonces f no tiene inversa y f-1 no existe.
Si f-1 existe, entonces:
1) f-1 es una función uno a uno.
2) Dominio de f-1 = Rango de f.
3) Rango de f-1 = Dominio de f.
Si f-1 existe, entonces:
1) x = f-1(y) sí y sólo si y = f(x).
2) f-1[f(x)] = x para toda x en el dominio de f.
3) f[f-1(y)] = y para toda y en el dominio de f-1 o, si x y y se han intercambiado, f[f-1(x)] = x para todax en el dominio de f.
FUNCIÓN ESCALONADA.-
Una función escalonada es aquella función definida a trozos que en cualquier intervalo finito [a,b] en que esté definida tiene un número finito de discontinuidades, y en cada intervalo es constante, teniendo discontinuidades de salto. Una función escalonada es aquella cuya gráfica tiene la forma de una escalera o una serie de escalones, al ser dibujadas ,algunas no necesariamente deben ser crecientes.
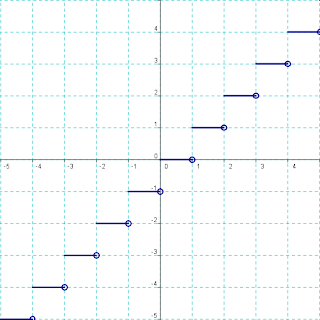
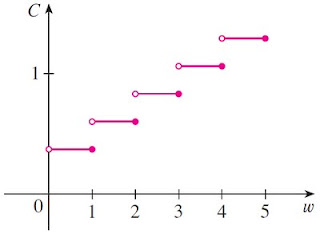
La función máximo entero se define por:
f(x) = [x] para el máximo entero menor o igual a x.
Ejemplos:
FUNCIÓN VALOR ABSOLUTO.-
La ecuación de la función de valor absoluto es f(x) = |x|. El dominio de la función valor absoluto es el conjunto de los números reales (R) y su rango es el conjunto de los números reales mayores o iguales que cero. Es decir:
Dominio = R
Rango = y≥0
Si x ≥ 0, entonces f(x) = x y al graficar es parte de la recta y = x, si x ≤ 0 entonces f(x) = -x y la gráfica de f es parte de la recta y = -x, la intersección y = x y y = -x, es el origen del sistema de coordenadas.
La función valor absoluto es decreciente en el intervalo (-∞, 0), creciente en (0, ∞) y es una función par por consiguiente, es simétrica con respecto al eje y.
Ejemplos:
f(x) = |x - 2|
f(x) = |x² -4x + 3|
x² -4x + 3 = 0 x = 1 x = 3
f(x) = |-x² + 5x - 4|
-x² + 5x - 4 =0 x² - 5x + 4 =0 x = 1 x = 4
f(x) = |x| − x
x = 0
f(x) = |x| / x
x = 0
FUNCIÓN IDENTIDAD.-
Es del tipo:
y = f(x) = x
Su gráfica es bisectriz del primer y tercer cuadrante.
Por tanto la recta forma con la parte positiva del eje de abscisas un ángulo de 45° y tiene de pendiente m = 1.
Sea f: R → r ,donde f(x) = x , esto es y = x. A esta función se le llama identidad o función idéntica.
Las características de la función identidad son:
1) El rango y el dominio de esta función son el conjunto de todos los números reales R.
2) Como el dominio (R) y el rango (R) son iguales, entonces la función identidad o idéntica es sobreyectiva.
3) Para toda x1 distinta de x2 se cumple que f(x2) ≠ f(x1) y, por tanto, la función es inyectiva.
4) En virtud que la función identidad es suprayectiva e inyectiva, entonces es biyectiva.
5) Para toda x1 > x2 tenemos que (x2) > (x1) por ende, la función identidad es creciente en el intervalo(-∞,∞).
Ejemplos:
°Graficar la siguiente función:
La ordenada al origen (3) nos indica que nos debemos parar sobre el eje y en el 3.
De ahí subimos 1 y avanzamos 2, como nos lo indica la pendiente.
°Graficar la función dada por f(x) = 2x – 1
Solución
Como la función es lineal se buscan dos puntos de la recta; para ello, se le dan valores a x y se encuentran sus imágenes respectivas, esto es:
Si x = 0, se tiene que f(0) = 2(0) – 1 = − 1
Si x = 2, se tiene que f(2) = 2(2) – 1 = 3
Así, los puntos obtenidos son (0, −1) y (2, 3), por los cuales se traza la gráfica correspondiente.
°Ahora el proceso inverso; o sea, si tenemos la gráfica de una función queremos encontrar su expresión analítica o matemática.
Para eso, necesitamos encontrar una expresión de la forma f(x) = ax + b a partir de la gráfica.
Por ejemplo, a partir de la siguiente gráfica, vamos a calcular su expresión matemática.
La imagen de 0 es b porque f(0) = a(0) + b = b luego b = –3
Tomamos otro punto, por ejemplo, el (2, 1); el 1 es la imagen del 2 luego se cumple que:
1 = a(2) + b → 1 = 2a – 3 → 4 = 2a → a = 2
Nuestra recta será: f(x) = 2x – 3
FUNCIÓN CONSTANTE.-
Se llama función constante a la que no depende de ninguna variable, y la podemos representar como una función matemática de la forma f(x) = c, donde c pertenece a los números reales y siempre permanecerá con el mismo valor es decir es una constante.
Ésta función es una recta horizontal en el plano cartesiano x. Si f(x) entonces y = c, donde c tiene un valor constante.
La función constante como un polinomio en x es de la forma f(x) = cx0.
Se dice que es constante porque su valor no cambia, a cada valor de x le corresponde siempre el valor de c.
Sea f: R → r ,cuya regla de correspondencia es f(x) = c, donde c es una constante, es decir, sea cual fuera el valor de x su imagen siempre es c.
La función f tiene las características siguientes:
1) El dominio de la función es el conjunto de todos los números relaes, es decir, Dom(f) = r .
2) El rango de la función es el conjunto {c}; por tanto, esta función no es sobreproyectiva.
3) La función tampoco es inyectiva, pues el conjunto de los pares ordenados que la forman tienen la misma imagen para cualquier valor de x.
4) Como la función no es sobreyectiva y no es inyectiva (uno a uno), tampoco es biyectiva y, por consiguiente, no tiene función inversa.
5) La función no es creciente ni decreciente: la función es constante.
6) La gráfica es el conjunto de todos los puntos en el plano que tienen ordenadas igual a c.
El dominio de la función constante va hacer igual siempre a "todos los reales" mientras que laimagen sólo va a ser el valor de c.
Una función constante es una función cuya fórmula es y = c, donde c es un número real. Su representación gráfica es una línea recta que corta al eje de ordenadas en el punto (0,c).
Las propiedades de las funciones constantes son:
-Una función constante es de la forma: f(x) = k, y tiene como gráfica una recta horizontal.
-El dominio de definición son todos los números reales X ϵ r.
-El rango sólo es un número y = k.
Ejemplo:
f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.
TRASLACIÓN DE GRÁFICAS.-
Los términos trasladar, deslizar, mover, y desplazar una gráfica, se utilizan como sinónimos.
En geometría, las transformaciones que mantienen la forma y el tamaño de una figura se denomina transformaciones las isométricas estas son:
Traslación desplaza la gráfica
Rotación gira la gráfica
Reflexión voltea la gráfica
La gráfica de muchas funciones son transformaciones geométricas de otras más simples.
La gráfica de y = x2 + 2 se obtiene trasladando la gráfica de y = x2 dos unidades hacia arriba, esto es una traslación vertical y puede ser hacia arriba o hacia abajo.
La gráfica de g(x) = (x + 2)2 se obtiene trasladando la gráfica de f(x) = x2 dos unidades hacia la izquierda, esto es una traslación horizontal y puede ser hacia la izquierda o hacia la derecha.
Traslación de la gráfica de f(x) cuando a > 0
Vertical
f(x) + a a unidades hacia arriba
f(x) - a a unidades hacia abajo
Horizontal
f(x + a) a unidades a la izquierda
f(x - a) a unidades a la derecha
La función g(x) = x + 3 se obtiene trasladando la gráfica de f(x) = x tres unidades hacia arriba y en el caso de la función h(x) = x - 3 se traslada tres unidades hacia abajo, esto es una traslación vertical.
La función g(x) = |x + 3| se obtiene trasladando la gráfica f(x) = |x| de tres unidades hacia la izquierda y en el caso de la función h(x) = |x - 3| se traslada tres unidades hacia la derecha, esto es una traslación horizontal.
Ejemplos:
°¿Cómo comparas las gráficas de y = x2 + 2 y y = x2 - 3 con la gráfica de y = x2? Observa las gráficas a continuación.
Observa que la gráfica de y = x2 + 2 sube dos unidades desde el origen y la gráfica de y = x2 - 3 baja tres unidades desde el origen.
°¿Cómo comparas las gráficas de y = (x + 2)2 y y = (x - 2)2 con la gráfica de y = x2? Observa las gráficas a continuación.
Observa que la gráfica de y = ( x + 2)2 se mueve dos unidades hacia la izquieda y la gráfica de y = (x - 2)2 se mueve dos unidades hacia la derecha.
No hay comentarios.:
Publicar un comentario