Una función polinomial general de grado n puede expresarse en la siguiente forma:
P(x) = anxn + an-1xn-1 + an-2xn-2 + … + a1x1 + a0x0
Donde a0,a1,a2 … an
FORMA POLINOMIAL DE FUNCIONES DE GRADOS: CERO, UNO Y DOS.-
Función polinomial de grado cero.-
Una función polinomial de grado cero es una función constante, su dominio es R y su rango es a0.
Si en la función polinomial general hacemos n = 0 resulta:
P(x) = a0x0 = a0
Ejemplo:
ƒ(x)=5
ƒ(x)=67
ƒ(x)=2
ƒ(x)=9
ƒ(x)=120
ƒ(x)=20
ƒ(x)=225
ƒ(x)=55
ƒ(x)=535
ƒ(x)=252
ƒ(x)=7
ƒ(x)=37
ƒ(x)=59
ƒ(x)=500
ƒ(x)=93756
ƒ(x)=82
ƒ(x)=105
ƒ(x)=8
ƒ(x)=79
ƒ(x)=89
Función polinomial de grado uno.-
Una función polinomial de grado uno es una función lineal, su dominio y su rango es R. La forma que se ha utilizado para referirse a una función de primer grado es f(x) = ax + b, aunque también suele escribirse como f(x) = mx + b, donde m = pendiente y b = ordenada al origen.
Si se considera n = 1 en la función polinomial general, resulta entonces la expresión:
P(x) = a1x1 + a0 = a1x + a0
Ejemplos:
ƒ(x)=2x+3
ƒ(x)=6x+5
ƒ(x)=24x-8
ƒ(x)=75x+90
ƒ(x)=57x-4
ƒ(x)=96x+32
ƒ(x)=253x+7849
ƒ(x)=3x+302
ƒ(x)=7x+68
ƒ(x)=18x+23
ƒ(x)=21x-1930
ƒ(x)=934+291
ƒ(x)=31x-274
ƒ(x)=56x-1745
ƒ(x)=222x-73
ƒ(x)23x-4
ƒ(x)=84x+74
ƒ(x)=8462x+5283
ƒ(x)=2973x+62
ƒ(x)=987x-938
Función polinomial de grado dos.-
La función polinomial de grado dos es conocida como función cuadrática, su dominio es R y su rango depende de los coeficientes de la función.
Algebraicamente puede expresarse utilizando diferentes formas, la forma general de la función cuadrática es: f(x) = ax2 + bx + c.
Otra forma de representar la función de segundo grado es la forma estándar, que puede obtenerse a partir de la forma general, que resulta más fácil de manejar para graficar, hacer traslaciones gráficas horizontales y verticales.
Partiendo de la expresión f(x) = ax2 + bx + c, y completando el trinomio cuadrado perfecto, según el siguiente procedimiento:
f(x) = a (x2 + b/a x) + c
f(x) = a [x2 + b/a x + (b/2a)2] - a (b/2a)2 + c
f(x) = a (x + b/2a)2 - a b2/4a2 + c
f(x) = a (x + b/2a)2 - b2/4a + 4ac/4a
Se obtiene que
f(x) = a (x + b/2a)2 + 4ac-b2/4a
Y si,
h = - b/2a
k = 4ac - b2/4a
La función resultante en f(x) = a (x - h)2 + k, queda en forma estándar.
Ejemplos:
f(x) = 23x2 + 78x + 2
f(x) = 2x2 + 2x + 6
f(x) = 7x2 + 96x + 9
f(x) = 12x2 + 162x + 12
f(x) = 432x2 + 988x + 45
f(x) = 58x2 + 25x + 14
f(x) = 6x2 + 4x + 63
f(x) = 13x2 + 64x + 452
f(x) = 9x2 + 8x + 4532
f(x) = 37x2 + 2354x + 6325
f(x) = 31x2 + 721x + 853
f(x) = 34x2 + 62x + 25457
f(x) = 78x2 + 93x + 6345
f(x) = 24x2 + 63x + 8273
f(x) = 90x2 + 74x + 242
f(x) = 36x2 + 132x + 163
f(x) = 20x2 + 90x + 976
f(x) = 178x2 + 34x + 80
f(x) = 25x2 + 7x + 79
f(x) = 79x2 + 3x + 25
REPRESENTACIÓN GRÁFICA DE FUNCIONES DE GRADOS: CERO, UNO Y DOS.-
Representación gráfica de funciones de grado cero.-
Su representación gráfica es:
Para a0 > 0
f(x) = a0
para a0 < 0
Dependiendo del valor de a0, la gráfica de la función puede ubicarse en el primer y segundo cuadrante, o en el tercer y cuarto cuadrante.
Representación gráfica de funciones de grado uno.-
Su representación gráfica corresponde a una línea recta. La forma que se ha utilizado para referirse a una función de primer grado es f(x) = ax + b, aunque también suele escribirse como f(x) = mx + b, donde m = pendiente y b = ordenada al origen.
Ejemplos:

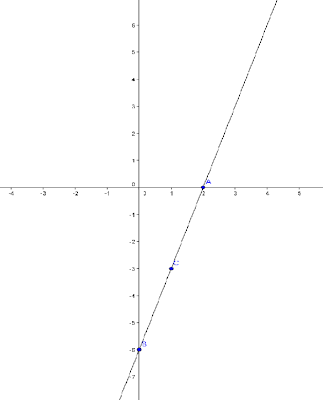
Representación gráfica de funciones de grado dos.-
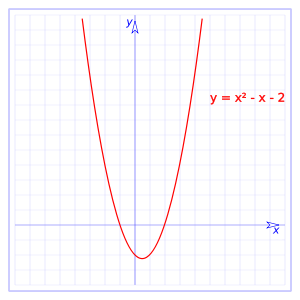
Un aspecto importante que se considera para construir el gráfico de una función es el cálculo de las intersecciones con los ejes, tanto x como y.
Para hallar la intersección con el eje y, es necesario igualar a x con cero y para hallar las intersecciones con el eje x, hay que igualar a y con cero.
En la gráfica, la intersección con y es el punto (0,c) y las intersecciones con el eje x son los puntos(r1,0) y (r2,0), donde r1 y r2 son las raíces de la función, que pueden obtenerse por diferentes métodos que van, desde el método gráfico, hasta diversos métodos algebraicos de factorización o la fórmula general. Las raíces r1 y r2 pueden ser reales o complejas. Cuando la gráfica de la función no corta al eje de las x, se dice que las raíces de la función son complejas.
Ejemplos:
Características de las funciones polinomiales de grado cero.-
Para a0 > 0
f(x) = a0
para a0 < 0
Características de las funciones polinomiales de grado uno.-
Una tabla corresponde a un modelo lineal si:
-Al comparar por cociente los datos de la tabla de la forma y/x resulta un valor constante m.
Un enunciado corresponde a un modelo lineal sí:
a) Se hace referencia a una variación directa.
b) Se establece una razón de cambio constante entre dos magnitudes.
Características de las funciones polinomiales de grado dos.-
Una tabla corresponde a un modelo cuadrático si:
a) Consta de al menos tres datos y a incrementos iguales de x las segundas diferencias de y son constantes, pero diferentes de cero.
Un enunciado corresponde a un modelo cuadrático si se hace mención:
a) A una relación cuadrática.
b) Al producto de dos factores lineales.
Parámetros de las funciones de grado cero.-
Dependiendo del valor de a0, la gráfica de la función puede ubicarse en el primer y segundo cuadrante, o en el tercer y cuarto cuadrante.
Parámetros de las funciones de grado uno.-
La pendiente y la ordenada al origen son dos parámetros importantes en la función lineal. La pendiente m indica la razón de cambio (rapidez con que cambia el valor de la función respecto a la variable independiente). Si se toma un intervalo de valores de x y hacemos la comparación por cociente de la variación de la función para ese intervalo, de la forma m = Δy/Δx y, obtenemos un resultado positivo, indica que la función es creciente y si el resultado es negativo indica que la función es decreciente.
Un número r es la raíz de una función lineal si cumple que f(r) = 0, es decir el valor de la variable independiente cuando la función toma el valor de cero.
0 = mx + b
Resolviendo para x queda que x = - b/m
Parámetro de las funciones de grado dos.-
f(x) = a(x - h)2 + k
El punto (h,k) es el vértice de la parábola, es también el punto donde la función alcanza su valor máximo o mínimo de acuerdo con el valor del coeficiente principal a.
Para a > 0, la función tiene un mínimo y su gráfica abre hacia la parte positiva del eje y.
Para a < 0, la función tiene un máximo y su gráfica abre hacia la parte negativa del eje y.
Ocurre que el vértice de la parábola constituye el punto donde la gráfica de la función cambia de decreciente a creciente si a > 0 y de creciente a decreciente si a < 0.
No hay comentarios.:
Publicar un comentario